慶應義塾大学大学院理工学研究科の和田凱渡大学院生(後期博士課程2年)、同大学理工学部物理情報工学科の山本直樹教授、東京大学素粒子物理国際研究センターの吉岡信行准教授らの共同研究グループは、量子コンピュータ上で実現される状態に対し、多数の物理量を効率的かつ高精度に測定する適応型量子アルゴリズムを開発しました。本手法は、理論上の最適精度である「ハイゼンベルグ限界」(注1) を達成すると同時に、計算時間や必要とされる量子ビット数に関して、大幅な改善を達成しました。本研究成果は、量子情報処理の実用化に向けた大きな一歩であり、誤り耐性量子計算の科学応用における礎となり、次世代量子アルゴリズムの基盤技術として、産業界および学術界に広く貢献することが見込まれます。
本研究の詳細は、2025年4月10日(米国東部夏時間)に、米国科学雑誌「PRX Quantum」のオンライン版に掲載されました。
本研究のポイント
- 量子コンピュータ上で準備される量子状態から、多くの物理量の「期待値」(注2) を効率的かつ高精度に測定する量子アルゴリズムを開発した。
- 量子力学の基礎理論で定められたハイゼンベルグ限界を達成するとともに、測定する物理量の個数に関しても量子的な加速を達成した。
- 量子状態に対する効率的な制御機構を設計し、計算の大幅なシンプル化を達成した。
- 本研究成果は、量子シミュレーション・量子機械学習などの幅広い応用先を持つことから、誤り耐性量子計算の科学応用における礎となることが期待される。
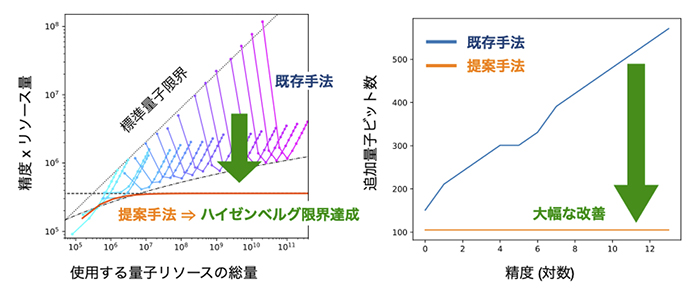
左図:精度と量子リソースの関係、右図:精度と追加量子ビット数の関係
研究背景
量子計算は、従来の計算手法と比較して圧倒的な性能を有する可能性を秘めていますが、計算結果を得るためには、必ず「測定」と呼ばれる最終工程が必要です。量子状態から情報を読み出すこの測定は、計算全体のパフォーマンスを左右する極めて重要なプロセスです。しかしながら、測定により、多くの計算タスクにおける最終出力である、複数の物理量の期待値を高精度に読み出す場合、従来の手法では非常に多くの量子リソースを必要とし、さらに、量子ビット数の観点でも膨大な追加リソースが求められることが課題でした。本研究では、量子リソースの効率的な配分と物理量の埋め込み手法を新たに再設計することで、測定精度を高め、量子ビット数の大幅な削減を同時に実現する、新たな量子アルゴリズムを提案し、従来手法が直面していた問題を解決しました。
研究内容・成果
本研究では、多くの物理量に関する期待値を、高精度かつ効率的に読み出すために、量子回路を動的に更新する「適応型アルゴリズム」(図2、注3) を構築しました。本手法は、量子状態に埋め込まれた関数の変化率(微分)を効率よく測定する既存手法を基盤とし、反復ステップを重ねるごとに、対象となる各物理量の期待値に生じる微小な変化をより正確に捉えることができます。この工夫により、使用する量子リソースの総量に対して、非常に高い精度の測定が実現できました。また、本手法では、ターゲットとなる量子状態の準備に必要な量子回路の使用回数が、目標とする精度に対して逆比例の関係を示しました。これは、量子性を最大限に活用した場合に達成可能な理論限界である「ハイゼンベルグ限界」を達成しており、通常手法が達成する「標準量子限界」(注4) での逆二乗の関係と比較すると、高精度の測定で必要となる量子リソースを大幅に削減できることを意味しています。提案手法ではさらに、従来よりも多数の(約2乗程度多くの)物理量を量子リソースの総量を増やすことなく測定できることを示しました。また、適応的なアルゴリズム構造を採用したことにより、測定精度を高めるために追加で必要だった量子ビット数も、従来手法と比べて1/5程度(もしくはそれ以上)まで削減できることを示しました (図1) 。
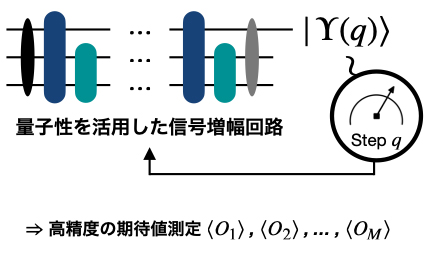
今後の展開
物理学者リチャード・ファインマンが量子シミュレーションの可能性を示して以降、現代では生み出された量子データから「どうやって物理的特性を効率的に取り出すか」という問いが次なる焦点となっています。本研究では、その自然かつ重要な問いへの回答として、シミュレートされた量子状態の多様な物理特性を、極めて効率よく測定できる汎用的手法を開発しました。その汎用性から、材料設計や創薬など、量子計算を活用するあらゆる分野で本手法は有効であり、誤り耐性量子計算の実用化を加速させることが期待されます。
原論文情報
タイトル:Heisenberg-Limited Adaptive Gradient Estimation for Multiple Observables
著者名:Kaito Wada, Naoki Yamamoto, Nobuyuki Yoshioka
雑誌名:PRX Quantum 6, 020308
DOI:https://doi.org/10.1103/PRXQuantum.6.020308
用語説明
- (注1) ハイゼンベルグ限界:量子測定手法に対するユニバーサルな理論限界。使用する量子リソースと測定精度の間の関係として定式化される。
- (注2) 期待値:ある量が平均的に取る値。
- (注3) 適応型アルゴリズム:測定結果などに応じて次の操作を柔軟に変えていく計算方法。
- (注4) 標準量子限界:通常の量子測定手法が示す、使用する量子リソースと測定精度の間の関係。
